Ley de seno y ley de coseno

Ley de senos y cosenos.

Ley de senos. La ley de senos es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos. Usualmente se nos presenta de la siguiente forma: Igualmente tenemos los despejes para cuando buscamos un lado y un ángulo respectivamente, añadiendo que al resultado de segundo despeje (el del ángulo) debemos sacarle seno inverso para que nuestro resultado sea correcto. Para poder usar la ley de senos debemos cumplir las siguientes condiciones: - Conocer un lado y dos ángulos del triángulo (LAA). - Conocer dos lados y el ángulo entre ellos (LLA). A continuación presento un ejemplo bastante sencillo usando un triángulo rectángulo. Tenemos el siguiente triángulo: Al ser un triángulo rectángulo, sabemos que el ángulo C mide 90 grados, nos indican que el ángulo A mide 45 grados por lo que podemos obtener el ángulo B restando la suma de estos dos valores a 180 grados; de esta manera sabemos que el ángulo B mide 45 grados. Después de realizar las operaciones obtenemos lo siguiente: Los pasos para resolver este triángulo son los siguientes: - Sabemos que es un triángulo LAA ya que conocemos el lado a y los ángulos A y C. - Despejamos nuestra razón de c sobre seno de C igual = a sobre seno de A; de esta manera encontraremos el valor del lado c. - Sustituimos nuestros valores en la fórmula que despejamos y obtenemos como resultado 16 por la raíz de 2. - Al ser un triángulo rectángulo podemos sacar el lado b directamente con el teorema de Pitágoras como lo hice en este ejercicio, aunque podríamos usar la ley de senos para obtenerlo. Ejercicio de aplicación. Una manera de aplicar la ley de senos es para obtener la altura de distintos objetos. En el siguiente caso la usaremos para obtener la altura de una torre de agua y una ventana. Tenemos como datos la distancia que hay desde el edificio a la torre de agua y dos ángulos que se forman desde la ventana hacia la base y la punta de la torre respectivamente, formando así dos triángulos rectángulos que resolveremos para obtener las alturas deseadas. Lo que podemos hacer en este caso es trazar ambos triángulos rectángulos; los pasos a seguir son los siguientes. - Para el primer triángulo sabemos que el ángulo A mide 39 grados y que el ángulo C mide 90 grados, para obtener el valor del ángulo B lo que hacemos es restar a 180 grados la suma de los otros dos y obtenemos como resultado 51 grados. - Realizamos nuestro despeje de la relación de lados y senos. - Sustituimos los valores dados en nuestra fórmula. - Obtendremos dos valores para a, si queremos conocer la altura total de la torre de agua debemos sumar ambos valores. - Si queremos conocer la altura de la ventana sólo usamos la altura del segundo triángulo que es el que está más cercano al suelo. Ley de cosenos. La ley de cosenos es una relación de un lado del triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados: Observamos cómo se utiliza la ley de cosenos cuando queremos buscar cualquier lado del triángulo, vemos que es muy parecido al teorema de Pitágoras; de igual forma tenemos el despeje de la fórmula cuando estamos buscando un ángulo del triángulo. Para poder utilizar la ley de cosenos debemos cumplir dos condiciones. - Tener dos lados del triángulo y el ángulo entre ellos. - Tener la medida de los tres lados del triángulo (donde usamos los despejes del lado derecho de la imagen). Incluyo un ejemplo donde utilicé la ley de cosenos para resolver el siguiente triángulo. Sé que puedo utilizar la ley de cosenos para resolver este problema ya que conozco la medida de los lados a y c, así como el ángulo que se encuentra entre ellos (B). Realizando las operaciones correspondientes obtuve lo siguiente: Los pasos para resolver el triángulo son: - Ya que estoy buscando el lado b del triángulo utilizo la fórmula de ley de cosenos para ese lado. - Sustituyo mis valores en la fórmula y realizo las operaciones obteniendo como resultado la raíz cuadrada de 139 y la dejo indicada así. - Ya que tengo los tres lados del triángulo puedo obtener ya sea el ángulo A o el ángulo C; en este caso encontré el valor del ángulo A. - Despejo la fórmula de ley de cosenos para mi ángulo A. - Sustituyo los valores dentro de mi fórmula despejada y realizo las operaciones. - Obtengo como resultado la medida del ángulo A que es de 12.83 grados. Para conocer la medida del ángulo C sin aplicar ley de cosenos es restar a 180 grados la suma de los valores de los ángulos A y B, de este modo sé que el valor del ángulo C es de 47.17 grados. Como conclusión a este tema puedo decir que al principio me costaba un poco de trabajo recordar las fórmulas de estas leyes, con un poco de práctica logré conocerlas mejor y saber en qué situaciones usar cada una de ellas; así como poder utilizarlas en distintos problemas de aplicación como medir alturas de edificios o distancias entre dos puntos conociendo sólo lados y ángulos de un triángulo. Además sé que no estoy casado con un solo método, puedo utilizar todos los recursos que tengo como estas leyes o el mismo teorema de Pitágoras. Teorema del coseno o de los cosenos Contenido de esta página: Introducción Teorema del coseno (enunciado y demostración) 6 Problemas resueltos de aplicación del teorema del coseno 1. Introducción El teorema del coseno (o teorema de los cosenos) es un resultado de trigonometríaque establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos. Este teorema es una generalización del teorema de Pitágoras (la razón de ello se encuentra en la nota del siguiente apartado). Para aplicar el teorema del coseno se necesita conocer la longitud de dos lados y la medida de un ángulo interior (opuesto al del otro lado). En esta página enunciamos y demostramos el teorema del coseno y resolvemos problemas de su aplicación en los que se pregunta por algún lado o ángulo de un triángulo dado. En algunos de los problemas se necesitan otros resultados básicos como el teorema de Pitágoras y la propiedad de que la suma de los ángulos internos de un triángulo es 180º. 2. Teorema del coseno Sea un triángulo cualquiera con lados $a$, $b$ y $c$y con ángulos interiores $\alpha$, $\beta$ y $\gamma$ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumplen las relaciones 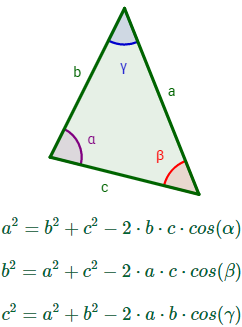Nota: se dice que es una generalización de Pitágoras porque si uno de los ángulos es recto, el triángulo es rectángulo, siendo la hipotenusa el lado opuesto a dicho ángulo y se obtiene el teorema de Pitágoras al aplicar el del coseno. Por ejemplo, si α = 90º, entonces, la primera de las tres fórmulas anteriores queda como $$a^2=b^2+c^2$$ siendo a la hipotenusa del triángulo. Ver demostración 6 Problemas Resueltos Notas previas: En el texto, escribiremos coseno de$x$ como $cos\left(x\right)$. También utilizaremos la función arcocoseno escrita como $arccos$, que es la función inversa del coseno. Normalmente, en las calculadoras esta función se denota por $co{s}^{-1}$. Problema 1 Se tiene un triángulo cuyos lados b y c miden 45 y 66 cm respectivamente y cuyo ángulo α mide 47°. Hallar cuánto mide el lado a del triángulo. 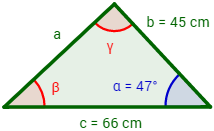Ver Solución Problema 2 Si cierto triángulo tiene un lado de 25.5 cm y otro de 37.5 cm y sus respectivos ángulos opuestos son de 37° y 62°, ¿cuánto mide el otro lado? Ver Solución Problema 3 ¿Cuál es el valor del ángulo γ del siguiente triángulo si se sabe que los lados a, b y c miden 6, 8 y 12 cm respectivamente? 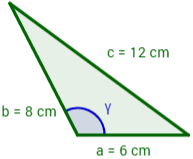Ver Solución Problema 4 Carlos y Felipe deciden competir en carreras alrededor de un parque. El parque tiene forma de triángulo con vértices A, B y C, ángulos α = 57° y γ = 76º y lados AC = 52 m y AB = 45 m. 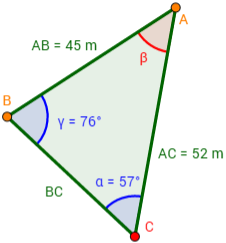Carlos parte del vértice A y Felipe parte del vértice B. La meta para ambos es el vértice C, pero cada uno debe pasar por el vértice del cual partió el otro antes de dirigirse hacia C. Si los dos corren a la misma velocidad y salen al mismo tiempo, ¿cuál de los dos amigos ganará la competición? Ver Solución Problema 5 Un labrador quiere comprar un terreno con forma triangular. Se le ofrecen dos terrenos colindantes: el terreno A y el terreno B. La longitud de las tres vallas que delimitan el terreno A son 18, 24 y 28 metros y las del terreno B son 19, 20 y 30 metros. 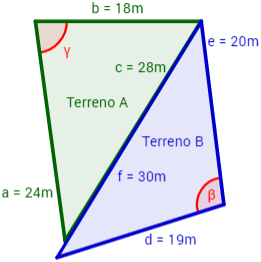¿Qué terreno debe comprar el labrador si desea el de mayor área? 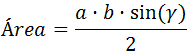Ayuda: el teorema del seno establece que el área de un triángulo de lados a, b, c y ángulo γ opuesto al lado c es Ver Solución Problema 6 El trayecto de un cuadriatlón (competición deportiva de cuatro disciplinas) está trazado entre cinco puntos (o vértices): A, B, C, D y E. 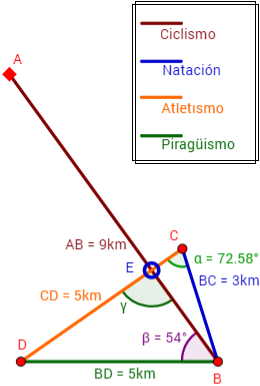El tramo AB son 9km de ciclismo, el tramo BCson 3km de natación, el tramo CD son 5km de atletismo y el tramo BD son 5km de piragüismo. En el vértice E hay una parada para tomar agua, la distancia entre los vértices C y E es de 0.95km y los ángulos α y β miden 72.58° y 54° respectivamente. Calcular: Distancias a (tramo EB) y b (tramo DE). Distancia del inicio a la parada a tomar agua (tramo AE). Ángulo γ. Ver Solución Resuelve en tu carpeta las siguientes situaciones problemáticas. Para ello ten en cuenta los conceptos señalados en la siguiente figura.  1) Una torre inclinada 10º respecto de la vertical, está sujeta por un cable desde un punto P a 15 metros de la base de la torre. Si el ángulo de elevación del cable es de 25º, calcula la longitud del cable y la altura de la torre. 2) Una persona observa un avión y un barco desde la cúpula de un faro, tal como muestra la figura.¿Cuál es la distancia que hay del barco al avión y del barco al observador? 3) Un hombre mide un ángulo de elevación de una torre desde un punto situado a 100 metros de ella. Si el ángulo medido es de 20º y la torre forma un ángulo de 68º con el suelo, determina su altura AB. 4) Dos autos parten de una estación y siguen por carreteras distintas que forman entre si un ángulo de 80º. Si las velocidades son 60 km/h y 100 km/h, ¿qué distancia los separa después de una hora y media de recorrido? 5) Un árbol es observado desde dos puntos opuestos separados 250 metros con ángulos de elevación de 30º y 25º. ¿Cuál es la altura del árbol y a qué distancia está de la cúspide de cada punto de observación? 6) Mariana observa un castillo desde su casa bajo un ángulo de 70º. Luego de unos minutos sale a dar un paseo y estando a 50 metros de su casa, observa el mismo castillo bajo un ángulo de 85º. ¿A qué distancia de ella y de su casa, se encuentra dicho castillo? Más problemas para resolver en tu carpeta 1) Un árbol está situado en la orilla de un río. El extremo superior del árbol, desde un cierto punto (ubicado en la otra margen del río), determina un ángulo de elevación de 17º. Si a 25 metros de dicho punto y en dirección al árbol, el ángulo es de 35º, ¿cuál es la altura del mismo? 2) Tres pueblos X, W y Z, están unidos por carreteras rectas. La distancia entre X y W es de 6 km; a los pueblos W y Z los separan 9 km. El ángulo que forman las carreteras que unen X con W y W con Z es de 120º. ¿Qué distancia hay entre X y Z? 3) En una plazoleta de forma triangular, los lados miden 60 m, 75 m y 50 m. ¿Qué ángulos se forman en las esquinas de la misma? 4) Calcular la longitud de la diagonal AC del hexágono regular ABCDEF, si el perímetro del mismo es de 72 cm